ラプラス変換 定義 条件
フーリエ変換逆変換の定義式は分野や文献によって異なる特に係数 1 2π を変換逆変換のどちらの係数とするかに差異が見られる. ラプラス変換 公式一覧 Jan 4 2019 on Math.
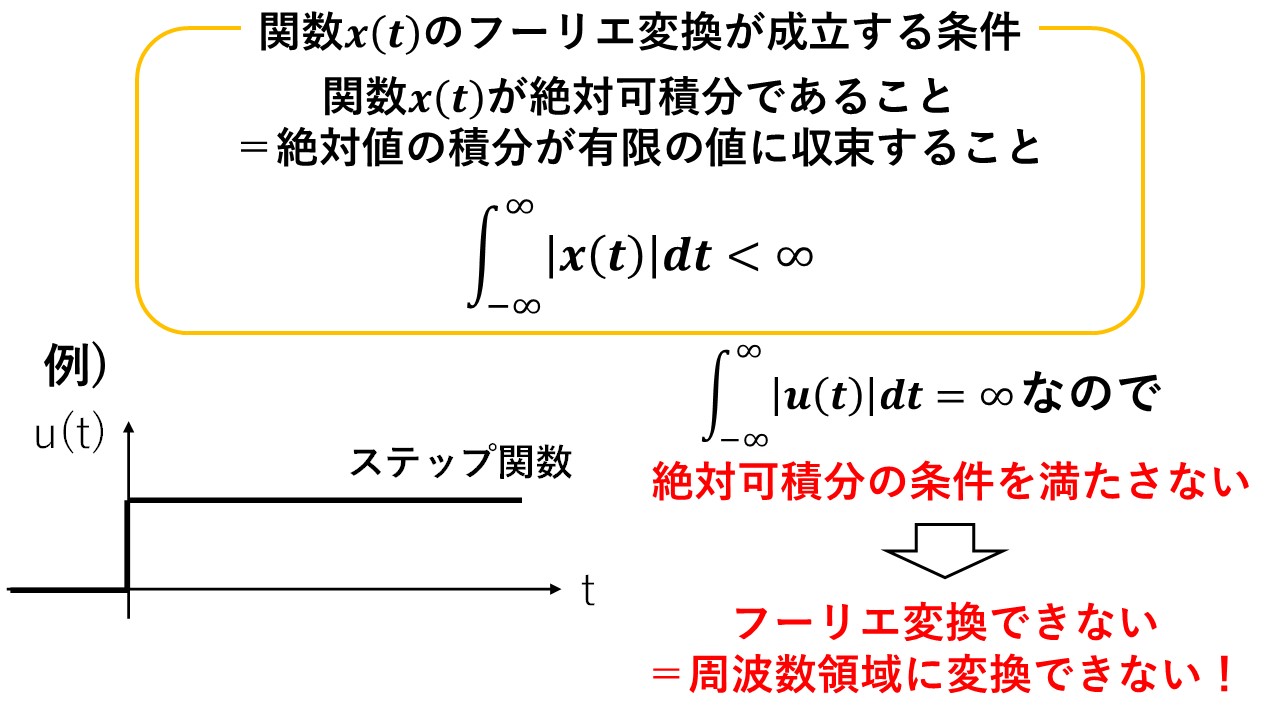
ラプラス変換を分かりやすく解説 ラプラス変換とフーリエ変換の違い ハヤシライスblog
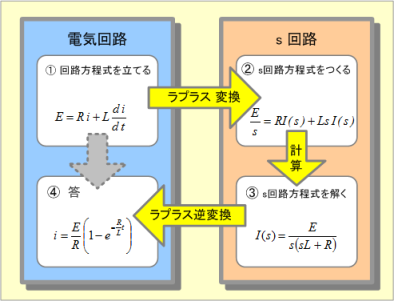
ラプラス変換とその使い方１ 基礎編 ラプラス変換とは何か 変換の基礎事項は 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会
これを ディラックのデルタ関数 とか 単位インパルス関数 とか 衝撃関数 といいます.
ラプラス変換 定義 条件. Step4逆ラプラス変換の表を参照しながらXsをxtにsの式をtの式に変換します Step5現れた式が微分方程式の解xtです ヘヴィサイドの解法は微分方程式を面倒な積分計算をしなくとも2つの表と代数的式変形だけで解いてしまう魔法です. ラプラス変換では 多数の広義積分を扱うことになるうえ ラプラス変換が存在する という条件が各種の定理についてまわることになる. T 0 の関数.
ここで とすれば良いので 2 変換表より. フーリエ変換逆変換の定義式は係数 1 2π を除けばt と ω を入れ替えただけで実質的に同じ式となる Note. 例 Ltsint を求めてみよう ラプラス変換の微分の式1225 によればsint のラプラス変換 Lsint s2 2 についてs微分を取り 1倍したものがそれに相当するので Ltsint d ds Lsint d ds.
2 ラプラス変換とは 本節では ラプラス変換 と 逆ラプラス変換 の定義を示しいくつかの 例題 を通して その 物理的なイメージ を探ります 21 定義狭義 時間 t 0 で定義された関数 f t について 以下に示す積分 F s を f t の ラプラス変換 といいます ここで t は実数 s は. ラプラス変換のイメージを絵的に説明するとラプラス変換によって得られる F sは f t と とを掛け合わせたものについて t 軸に挟まれた t 0 からまでの面積と考えることができます. を意味しているここでもフーリエ変換を使ってグリーン関数を求めてみよう今度は時間ではなく 空間座標でフーリエ変換を行うつまり UK ureiKrd3r 27 ur 1 2π 3 UKeiKrd3K 28 で定義するまたラプラス方程式のグリーン関数は G δ.
本記事からラプラス変換の解説を始めていく フーリエ変換と同様にラプラス変換もある関数を別の関数に写像する操作である ラプラス変換を利用すると微分方程式を容易に解くことができる概要 0leq tinftyで定. この記事から数回にわたって定積分について学んでいきます 不定積分についてはこちら 不定積分の定義と公式有理関数三角関数無理関数の不定積分 目次 1 定積分11 リーマン和12 リーマン積分可能2 積分可能性の判定条件21. Laplace 変換とラプラス逆変換 復習 ラプラス変換とラプラス逆変換 復習 ラプラス変換L の定義 ft.
Laplacianはユークリッド空間上の函数の勾配の発散として与えられる微分作用素である 記号では 2 あるいは で表されるのが普通である 函数 f の点 p におけるラプラシアン. この関数の重要な性質として ft を -infty infty で定義された任意の連続関数としたとき次が成り立ちます. デルタ関数と ラプラス変換 松尾孝美 平成 年 月 日 変換の定義と意義 片側ラプラス変換は でゼロである信号因果性関数線形モデルおよび制御システムを解析するために広く用.
S2 2 2s s2 22. 1 のラプラス変換を求めよ t倍法則を利用する 2 のラプラス変換を求めよ 線形法則と移動法則を利用する 3 のラプラス変換を求めよ 移動法則を利用する f t 3e2t 5 f t tsinat f t e2t cos3t 2 2 sin s a a L at 2 cos s a s L at 4 微分法則で より を導こう. 実数とするときLfs Z 0 est ftdt ラプラス逆変換L1 の定義L1Fs ft Lft Fs 線形性.
具体的に図を使って説明すると図2-1-3のグラフは時間関数 f tと とを掛け合わせたものラプラス積分. 1228 124 ラプラス変換と微分方程式 微分のラプラス変換の式を応用することで微分. 高専4年の数学の教科書として使用した新 応用数学大日本図書 のラプラス変換についての公式などを備忘録としてまとめたものです 21 ラプラス変換の定義と性質 定義.
どうも木村kimu3_slimeです 今回はラプラス変換とは何かその定義と微分方程式への応用を紹介します 手っ取り早く全体像をつかむための導入なので公式の導出などは一旦省. そのため このような判定方法を知っておくことは これから行おうとする計算にラプラス変換の各種の定理を用いてよいかどうかの判断材料を増やすことに. 関数f1t f2tF1s F2s と定数c1c2 に対してLc1f1tc2f2t.
ところで② 逆ラプラス変換との関係は 上記ではz変換によって周波数領域時間領域への変換を行っていますが逆ラプラス変換によっても行うことが出来ますこの場合と離散時間状態方程式との差異についても気になったので明らかにしてみます. 未定係数法で解く 1 とおく ゆえに. Laplace transform とは積分で定義される関数空間の間の写像線型作用素の一種 関数変換 ラプラス変換の名はピエールシモンラプラスにちなむ.
これもまたラプラス変換のときと同様に Z 変換後の関数 F z を伝達関数と呼びます ラプラス変換の F s も伝達関数と呼ぶため この2つを同時使う場合には F s をアナログ伝達関数 F z をディジタル伝達関数などといって区別する場合もあります ディジタル信号処理における.
ラプラス変換 理系ノート
ラプラス変換の復習 教科書には相当する章はない Ppt Download
ラプラス変換 Emanの物理数学
2
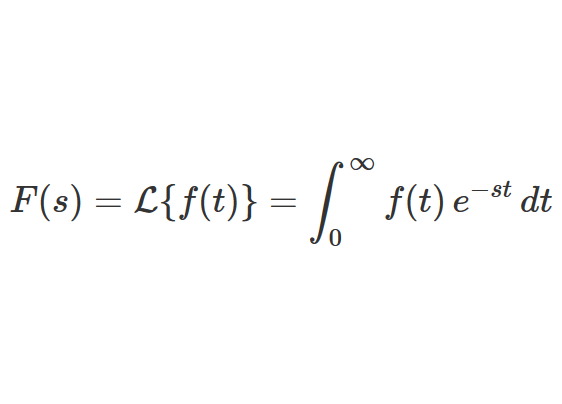
電気数学のお勉強 ラプラス変換
1
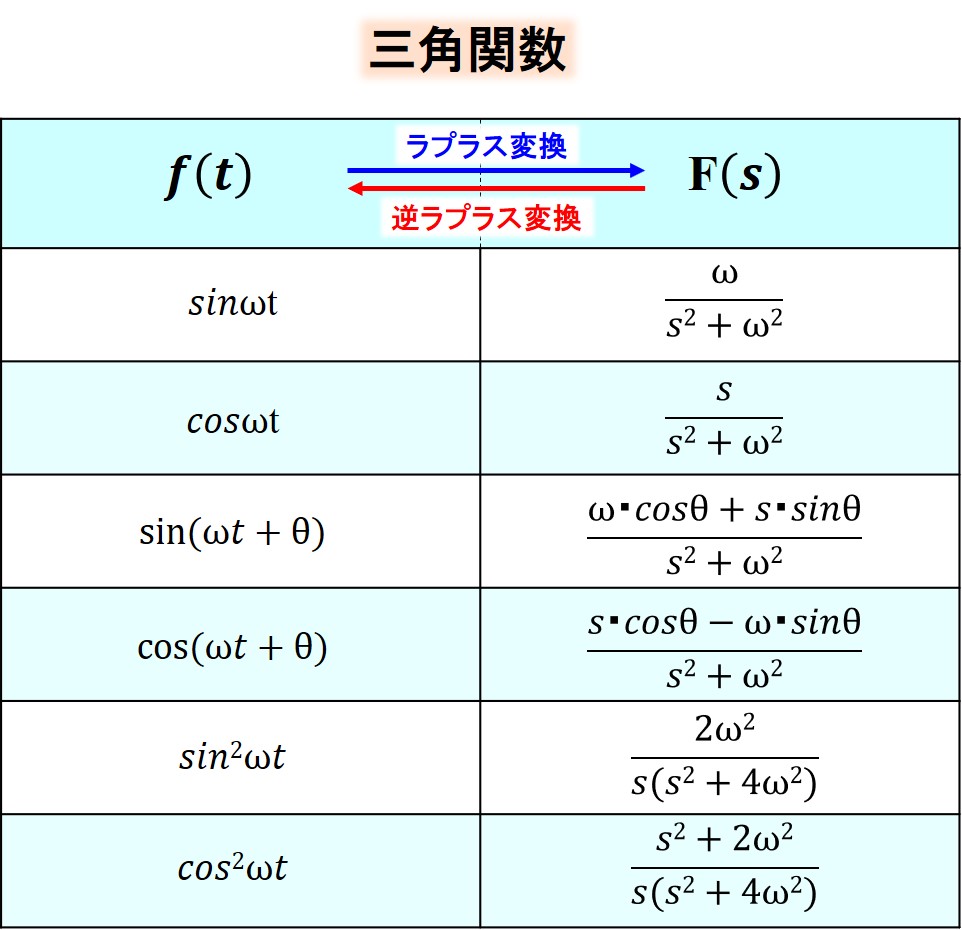
ラプラス変換をわかりやすく 変換表を知ろう 物理講師デルタ先生の部屋
ラプラス変換表
You have just read the article entitled ラプラス変換 定義 条件. You can also bookmark this page with the URL : https://cookiel012o.blogspot.com/2022/05/blog-post_489.html
0 Response to "ラプラス変換 定義 条件"
Post a Comment